[열역학] 1.열역학 제 1 법칙과 내부 에너지(Internal Energy), 엔탈피(Enthalpy)

지난 글에서 열역학의 기본 개념과 열역학만의 표기법, 수학적 배경 지식에 대해 다루고 있으니 읽고 오는 것을 추천한다.

https://sidreco.tistory.com/32

[열역학] 열역학의 공리와 기본 개념

 

열역학 제 0 법칙

두 물체가 열적 평형을 이루었다면, 두 물체의 온도는 같다.

상식적이라고도 할 수 있는 내용이다.

일 (Work)

일의 정의에 따라 힘의 방향이 일정할 때 \(\Delta W = F \times \Delta x\)로 표현된다. 이를 압력과 부피로 표현하면 다음과 같다.

$$ \Delta W = F \times \Delta x = \dfrac{F}{A} \times A \Delta x = P \Delta V $$

극한을 취하면

$$ \dfrac{dW}{dV} = P $$

$$ W = \int_{V_1}^{V_2} P dV $$

이때 일은 경로에 따라 달라지는 경로 함수이므로 물리학에서는 이를 아래와 같이 표현한다.

$$ \delta W = P dV $$

*참고로 이는 부피변화에 의한 일만을 고려한 것이다. 일은 에너지의 이동 형태이므로 화학적 일이나 전자기적 일등 다른 일을 도입할 수도 있다.

*여기서는 계가 주위에 일을 하였을 때 일의 부호를 +로 하여 다루고 있지만, 다른 분야(특히 화학)에서는 이를 반대로 정의하니 참고할 것

열역학 제 1 법칙과 내부 에너지

에너지가 보존되려면, 순환 과정에서 계가 흡수한 열만큼 일을 해야 할 것이다. 이를 순환적분을 사용해서 수식으로 표현하면 다음과 같다.

$$ \oint_C \delta Q = \oint_C \delta W $$

이항하면

$$ \oint_C (\delta Q - \delta W) = 0 $$

이 되는데, 아래 그림처럼 폐곡선 \(C\)를 둘로 나누면

 

$$ \int_{C_1} (\delta Q - \delta W) + \int_{C_2} (\delta Q - \delta W) = 0 $$

$$ \int_{C_1} (\delta Q - \delta W) = \int_{-C_2} (\delta Q - \delta W) $$

\( \delta Q - \delta W \)가 경로 독립인 함수의 정의, 즉 상태 함수라는 것을 알 수 있다. 따라서 이를 내부 에너지 (internal energy) \(U\)라고 아래와 같이 정의 하자.

$$ dU \equiv \delta Q - \delta W $$

위 정의로 부터 열역학 제 1법칙이 정의 된다.

$$ \delta Q = dU + \delta W $$

이 식을 말로 풀어쓰면 들어온 열은 내부 에너지 증가와 일에 사용된다는 것이다. 그리고 이 식으로 부터 내부 에너지가 열과 일의 형태의 에너지를 제외한 물질이 가진 다른 모든 에너지를 뭉뚱그려 표현한 것임을 알 수 있다. (열과 일은 에너지의 이동 형태에 지나지 않는다.)

열역학 과정

●등적(等積) 과정 (isochoric process)

여기서 적은 부피를 의미하므로 일정한 부피에서 진행되는 열역학 과정이다. 참고로 choric은 ~에 속하는 이다.

https://en.wikipedia.org/wiki/Isochoric_process

●정압(定壓) 과정 (isobaric process)

한자에서도 드러나고, 영어에서도 bar는 압력을 의미하므로 일정한 압력에서 진행되는 열역학 과정임을 알 수 있다.

https://en.wikipedia.org/wiki/Isobaric_process

●등온(等溫) 과정 (isothermal process)

일정한 온도에서 진행되는 열역학 과정이다. 이상기체의 경우 \(P = \dfrac{nRT}{V} \)이므로 반비례 함수의 그래프를 그린다.

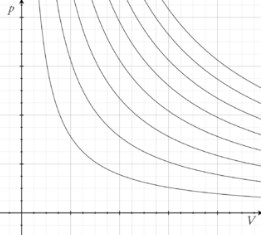
https://en.wikipedia.org/wiki/Isothermal_process

●단열(斷熱) 과정 (adiabatic process)

열이 출입하지 않는 과정이다. 열이 이동할 틈이 없이 순식간에 일어나거나, 주위가 진공이고 물체의 온도가 흑체 복사를 무시할 수 있을 만큼 낮다면 단열 과정으로 생각할 수 있다.

https://en.wikipedia.org/wiki/Adiabatic_process

엔탈피 (Enthalpy)

우리 주변의 대부분의 현상은 일정한 압력(대기압) 하에서 일어난다. 그러므로 열역학 제 1 법칙을 일정 압력이라는 상황에서 적용시켜보자. 출입한 열량은 경로 함수이므로 일정 압력이라는 것을 나타내기 위해 \(\delta Q_p\)라고 표기를 한다.

$$ \delta Q_p = dU + dW = dU + PdV = d(U + PV) $$

$$ H \equiv U + PV $$

라고 새로운 상태 함수를 정의한다면 일정 압력하에서 일어나는 현상을 보다 편하게 기술할 수 있을 것이다.

또한 정의에 따라 \(dH = \delta Q_p \)가 되므로 출입한 열량을 측정한다면 엔탈피 변화를 알 수 있게 된다.

 

열용량 (Heat Capacity)

열용량은 물체의 온도를 1 k만큼 올리기 위해 필요한 열량이며, 아래와 같이 정의된다.

$$ C \equiv \dfrac{ \delta Q}{d T} $$

여기서 출입한 열량은 경로 함수이므로, 일정 부피인 경로와 일정 압력인 경로 2가지를 생각해보자. 먼저 일정 부피에서는 \(\delta Q_v = dU\)가 되므로

$$ C_v = \dfrac{\delta Q_v}{dT} =  \left( \dfrac{ dU }{dT} \right)_V = \left( \dfrac{\partial U}{\partial T} \right)_V $$

이때 질량이 일정하다면 변수는 \(P, V ,T\)인데, \(V, T\)가 정해지면 남은 한 변수는 state postulate에 의해서 정해지므로 내부에너지는 \(V, T\)에 대한 이변수 함수가 된다. 그러므로 

$$ \dfrac{dU}{dT} = \left( \dfrac{\partial U}{\partial T} \right)_V + \left( \dfrac{\partial U}{\partial V} \right)_T \dfrac{dV}{dT} $$

부피가 일정하므로 \( \left( \dfrac{ dU }{dT} \right)_V = \left( \dfrac{\partial U}{\partial T} \right)_V \)이 된다.

 

같은 방법으로 일정 압력에선 \(\delta Q_p = dH \)가 되고, 엔탈피를 \(T, P\)에 대한 함수로 표현하면 아래와 같이 식이 전개 된다.

$$ C_p = \dfrac{\delta Q_p}{dT} =  \left( \dfrac{ dH }{dT} \right)_P = \left( \dfrac{\partial H}{\partial T} \right)_P $$

 

정적 열용량과 정압 열용량 사이 관계

정압의 경우 정적과 달리 온도로 올리고 외부에 일도 하므로 항상 정압 열용량이 정적 열용량보다 클 것임을 떠올릴 수 있을 것이다. 고체와 액체의 경우 열팽창이 크지 않으니 크게 차이나지 않지만, 기체의 경우 무시할 수 없게 된다. \(U = U(T, V) \), \(H = H(T, P) \)로 두고, 열역학 제 1 법칙을 이용해서 두 열용량 사이의 관계를 알아보자

$$ \begin{align} C_p &= \dfrac{\delta Q_p}{dT} = \left( \dfrac{dU}{dT} + P \left( \dfrac{dV}{dT} \right) \right)_P\\ &= \left( \dfrac{ \partial U}{ \partial T} \right)_V + \left( \dfrac{\partial U}{\partial V} \right)_T \left( \dfrac{dV}{dT} \right)_P + P \left( \dfrac{dV}{dT} \right)_P \\ &= C_v + \left[ \left( \dfrac{\partial U}{\partial V} \right) + P \right] \left( \dfrac{\partial V}{\partial T} \right)_P \end{align} $$

*\(V = V(T, P) \)인데 \(P\)가 고정이므로 \( \left( \dfrac{dV}{dT} \right)_P = \left( \dfrac{\partial V}{\partial T} \right)_P \)가 된다.

 

이상기체의 경우 에너지 등분배 정리(Energy Equipartition Theorem)에 따라 \(U = \dfrac{f}{2} N k_b T \) ( \(f\)는 자유도, \(N\)은 입자수, \(k_b\)는 볼츠만 상수 )이므로 온전히 \(T\)에 대한 함수이다. 그러므로 \( \left( \dfrac{ \partial U}{\partial V} \right)_T = 0 \)이 되며, 이상기체 상태 방정식 \(PV = nRT\)로 부터 아래의 식을 얻게 된다.

$$ C_p = C_v + nR $$

몰당 양이라는 것을 bar로 나타내어 아래와 같이 쓸 수 있다.

$$ \bar{C}_p = \bar{C}_v + R $$

*에너지 등분배 정리에 대해서는 아래 글을 참고하면 된다.

https://sidreco.tistory.com/20

맥스웰-볼츠만 분포(Maxwell-Boltzmann Distribution)

 

 

이상 기체의 단열 과정

이상 기체의 단열 과정은 다음과 같은 관계를 가진다.

$$ T V^{\gamma -1} = \text{constant},\ \gamma = \dfrac{ \bar{C}_p }{ \bar{C}_v } $$

몰수가 일정하다면 \(PV = nRT\)에서 아래와 같은 관계식이 나온다.

$$ PV^{\gamma} = \text{constant}$$

 

열역학 제 1 법칙으로부터 이를 유도해보자. 단열이므로 \(\delta Q = 0\)가 된다.

$$ dU = - P dV $$

$$ \dfrac {dU}{dV} = -P $$

$$ \left( \dfrac{\partial U}{\partial T} \right)_V \dfrac{dT}{dV} + \left( \dfrac{\partial U}{\partial V} \right)_T = -P $$

$$ C_v \dfrac{dT}{dV} = - \dfrac{nRT}{V} $$

$$ \dfrac{\bar{C}_v }{T} \dfrac{dT}{dV} = - \dfrac{R}{V} $$

\(\gamma\)의 정의와 \(\bar{C}_p = \bar{C}_v + R \)를 이용하면 \(R = (\gamma -1) \bar{C}_v \)이므로

$$ \dfrac{1}{T} \dfrac{dT}{dV} = - \dfrac{\gamma -1 }{V} $$

양변을 \(V\)에 대해 적분하면

$$ \ln{T} = - (\gamma -1) \ln{V} + K $$

여기서 \(K\)는 적분 상수이다. \( \ln{ T V^{\gamma -1} } = K \)이므로

$$ T V^{\gamma -1} = \text{constant} $$

임을 알 수 있다.

 

Summary

일 (P-V only)

$$ \delta W = P dV $$

내부 에너지 (internal energy)

$$ dU \equiv \delta Q - \delta W $$

엔탈피 (Enthalpy)

$$ H \equiv U + PV $$

 

열역학 제 1 법칙

$$ \delta Q = dU + \delta W $$

 

열용량

$$ C \equiv \dfrac{ \delta Q}{d T} $$

정적 열용량

$$ C_v = \left( \dfrac{\partial U}{\partial T} \right)_V $$

정압 열용량

$$ C_p = \left( \dfrac{\partial H}{\partial T} \right)_P $$

 

정압 열용량과 정적 열용량 사이 관계

$$ C_p = C_v + \left[ \left( \dfrac{\partial U}{\partial V} \right) + P \right] \left( \dfrac{\partial V}{\partial T} \right)_P  $$

 

이상기체의 단열 과정

$$ T V^{\gamma -1} = \text{constant},\ \gamma = \dfrac{ \bar{C}_p }{ \bar{C}_v } $$

몰수가 일정할때 이상기체의 단열 과정

$$ PV^{\gamma} = \text{constant}$$

 

참고문헌

Gilbert W. Castellan, Physical Chemistry 3rd ed