[양자역학] 8.Valance Bond Theory와 Hybrid Orbital + 시각화

지난글에서는 수소꼴 원자의 오비탈을 슈뢰딩거 방정식을 풀어서 구해보고, python으로 시각화도 해보았다. 이번글에서는 일반화학 강의때 들어보았을 Hybrid Orbital에 대해서 알아볼 것이다.

 

Born Oppenheimer Approximation

핵은 전자에 비해서 아주 느리게 움직이기 때문에 핵들은 임의의 간격으로 고정되어 있다고 가정하고 방정식을 풀이하는 것이다. 

 

Valance Bond Theory

스핀이 다른 두 고립 전자(unpaired electron)를 생각해보자. 두 원자핵의 거리가 매우 가깝다면, 전자는 1번 원자의 파동함수에 속할 수도 있고, 2번 원자의 파동함수에 속할 수도 있을 것이다. 그런데 두 가지 경우에 대해 구별이 불가능하므로 이를 중첩으로 표현하는 것이 올바른 표현이다.

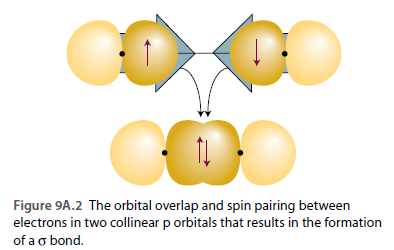
Sigma 결합

파동함수가 중첩될 때 위와 같이 직접 겹치는 방식으로 중첩되는 경우 \(\sigma\) 결합이라 부른다.

 

Pi 결합

그리고 위의 그림처럼 평행하게 중첩되는 경우 \(\pi\) 결합이라 부른다.

http://contents.kocw.or.kr/KOCW/document/2016/pusan/kimtaekyu/10.pdf

 

그런데 이와 같은 초기 Valance Bond Theory는 2가지 문제점이 있다.

1. 탄소가 4개의 결합이 가능하다는 사실을 설명하지 못한다.

탄소는 \(2s^2 2p^2 \)이므로 짝짓지 않은 전자가 2개 뿐이다. 그러므로 Valance Bond Theory에 따르면 2개의 결합밖에 형형하지 못할 것이다.

2. 물의 결합각을 설명할 수 없다.

p 오비탈들은 90도를 이루므로, 초기 Valance Bond Theory로 예측한 물의 결합각은 90도 이지만 실제로는 104.5도의 결합각을 가진다. 

 

그래서 Valance Bond Theory 에서는 Promotion과 Hybridization이라는 두 개념을 도입하였다. 먼저 Promotion은 s 오비탈의 전자가 p 오비탈로 들뜸(excited)으로서 \(2s^1 2p_x^1 2p_y^1 2p_z^1 \)가 되어  4개의 고립 전자를 만든다는 것이다. 그리고 결합이 형성되면서 들뜨는데 사용했던 에너지보다 더 많은 에너지를 방출하여 안정화된다. 다만 이는 결합이 일어날 때 에너지가 살짝 올랐다 내려가는 현상에 대한 개념적인 설명이며, 실제 일어나는 과정은 아니다.

 

그리고 Hybridization은 s오비탈과 p 오비탈의 선형 결합을 통해 혼성 오비탈(Hybrid Orbital)을 만든다는 것으로, 현상에 이론을 끼워맞춘 것이다. 아래서 어떻게 끼워맞추었는지 살펴보자

 

SP3 Hybrid Orbital

\(p_x, p_y, p_z \) 오비탈은 각각 \(x, y, z\)방향을 향해있으며, 서로 90도를 이룬다. 그런데 실제 현상은 결합각 109.5도의 정사면체를 이루므로, \( (1, 1, 1)\) 방향을 가르키는 오비탈을 h1이라고 하면 아래와 같이 표현된다.

$$ h_1 = as + b(p_x + p_y + p_z) $$

(미지수를 4개로 두고 모든 혼성오비탈이 직교하도록 계수를 찾아도 되지만, 모양을 보면 직관적으로 p오비탈들이 \(1:1:1\)로 더해져야된다는 것을 알 수 있다.)

그리고 \( (0, 0, 1) \) 방향은 \(-1:-1:1\)로 결합하면 되니 다음과 같다.

$$ h_2 = as + b(-p_x - p_y + p_z) $$

같은 방법으로 \( (0, 1, 0) \), \( (1, 0, 0) \)을 향하는 혼성오비탈은 다음과 같다.

$$ h_3 = as + b(-p_x + p_y - p_z) $$

$$ h_4 = as + b(p_x - p_y - p_z) $$

여기서 4개가 모두 혼성화 되었으므로 서로 직교해야한다.

$$ \int h_1^* h_2 d \tau = \int h_1 h_2 d\tau = (a-b)(a+b) = 0 $$

\(a=b\) 또는 \(a=-b\)인데, 둘중 어떤걸 택하는 공간상에서 회전시키면 같은 모양이 나타난다. 편의상 \(a=b\)라 해보자. 

책에는 위에 처럼 나와있는데, \(s, p_x, p_y, p_z \)오비탈이 모두 직교하고, 같은걸 내적하였을 때는 값이 1이므로, 정규화를 거치면 다음과 같다.

$$ h_1 = \dfrac{1}{2} (s + p_x + p_y + p_z) $$

$$ h_2 = \dfrac{1}{2} (s - p_x - p_y + p_z) $$

$$ h_3 = \dfrac{1}{2} (s - p_x + p_y - p_z) $$

$$ h_4 = \dfrac{1}{2} (s + p_x - p_y - p_z) $$

오비탈의 모양을 보는데는 굳이 정규화를 안해도 되고, Valance Bond Theory는 분자의 에너지를 계산하는데는 사용하지 않기 때문에 정확하게 구하지 않은 것으로 추측된다.

 

SP2 Hybrid Orbital

관습적으로 \(p_z\) 오비탈을 남겨두고 \(p_x\), \(p_y\)오비탈을 선형결합시켜 나타낸다.

그림처럼 \(p_x, p_y\)오비탈을 \(x, y\)축에 대한 기저로 보고 아래와 같이 \(h_1\)을 정의하자 (정규화를 거칠 것이니 s오비탈 앞의 계수는 1로 두어도 된다.)

$$h_1 = s + a p_y $$

120도 반시계 방향 회전변환 행렬은 다음과 같다.

$$ R = \begin{bmatrix} \cos \left( \dfrac{2}{3}\pi \right) && - \sin \left( \dfrac{2}{3}\pi \right)\\  \sin \left( \dfrac{2}{3}\pi \right) && \cos \left( \dfrac{2}{3}\pi \right) \end{bmatrix} = \begin{bmatrix} -\dfrac{1}{2} && -\dfrac{\sqrt{3}}{2}\\ \dfrac{\sqrt{3}}{2} && -\dfrac{1}{2} \end{bmatrix} $$

회전변환 행렬은 역행렬이 전치행렬인 직교 행렬이므로 \(h_2\)와 \(h_3\)는 다음과 같다.

$$ h_2 = s + \begin{bmatrix} -\dfrac{1}{2} && \dfrac{\sqrt{3}}{2}\\ -\dfrac{\sqrt{3}}{2} && -\dfrac{1}{2} \end{bmatrix} \begin{bmatrix} 0 \\ a \end{bmatrix} = s + a \begin{bmatrix} \dfrac{\sqrt{3}}{2}\\ -\dfrac{1}{2} \end{bmatrix} = s + a\left( \dfrac{\sqrt{3}}{2} p_x - \dfrac{1}{2} p_y \right) $$

$$ h_3 = s + \begin{bmatrix} -\dfrac{1}{2} && -\dfrac{\sqrt{3}}{2}\\ \dfrac{\sqrt{3}}{2} && -\dfrac{1}{2} \end{bmatrix} \begin{bmatrix} 0 \\ a \end{bmatrix} = s + a \begin{bmatrix} -\dfrac{\sqrt{3}}{2}\\ -\dfrac{1}{2} \end{bmatrix} = s + a\left( -\dfrac{\sqrt{3}}{2} p_x - \dfrac{1}{2} p_y \right) $$

SP3와 달리 직교하지 않는다는 것을 알 수 있다.

$$ \int h_1^* h_1 d\tau =  \int h_2^* h_2 d \tau =  \int h_3^* h_3 d\tau = 1 + a^2 $$

이므로 \(a= \sqrt{2}\)라고 한뒤 전체를 3으로 나누어주면 nomailization을 할 수 있다.

$$h_1 =  \dfrac{1}{3} \left( s + \sqrt{2} p_y \right) $$

$$h_2 =  \dfrac{1}{3} \left( s + \sqrt{ \dfrac{3}{2} } p_x - \sqrt{ \dfrac{1}{2} }p_y \right) $$

$$h_3 =  \dfrac{1}{3} \left( s - \sqrt{ \dfrac{3}{2} } p_x - \sqrt{ \dfrac{1}{2} }p_y \right) $$

 

참고로 책에서는 nomailization을 하지 않았다.

 

SP Hybrid Orbital

앞의 SP3, SP2와 달리 매우 간단하다

$$h_1 = \dfrac{1}{ \sqrt{2} } \left( s + p_z \right) $$ 

$$h_2 = \dfrac{1}{ \sqrt{2} } \left( s - p_z \right) $$

 

 참고로 책에서는 nomailization을 하지 않았다.

 

Visualization

Hybriz Orbital을 시각화하기 위해서 지난번에 수소꼴 원자에서 사용했던 코드를 조금 바꾸었다.

import math
import numpy as np
import scipy.special as spe
import matplotlib.pyplot as plt

#radial function
def R(n, l, r):
    coeff = np.sqrt( (2.0/n)**3 * math.factorial(n-l-1)/(2.0*n*math.factorial(n+l)) )
    
    #associated laguerre
    #https://docs.scipy.org/doc/scipy/reference/generated/scipy.special.assoc_laguerre.html
    laguerre = spe.assoc_laguerre(2.0*r/n, n-l-1, 2.0*l+1)
    return coeff * (2.0*r/n)**l * np.exp(-r/n) * laguerre

#wavefunction
def psi(n:int, l:int, m:int, r:float, elev:float, azim:float)->complex:
    """Hydrogenic Wave Function

    Args:
        n (int): principal quantum number
        l (int): azimutal quantum number
        m (int): magnetic quantum number
        r (float): radius
        elev (float): elevation angle
        azim (float): azimutal angle

    Returns:
        complex: value
    """
    #spherical harmonic
    #https://docs.scipy.org/doc/scipy/reference/generated/scipy.special.sph_harm.html
    return R(n, l, r) * spe.sph_harm(m, l, azim, elev)

def psi_real(n:int, l:int, m:int, r:int, elev:float, azim:float)->float:
    """Hydrogenic Wave Function (Real)

    Args:
        n (int): principal quantum number
        l (int): azimutal quantum number
        m (int): magnetic quantum number
        r (float): radius
        elev (float): elevation angle
        azim (float): azimutal angle

    Returns:
        complex: value
    """
    
    if m == 0:
        return psi(n, l, m, r, elev, azim)
    elif m > 0:
        return np.sqrt(2)*np.real(psi(n, l, abs(m), r, elev, azim))
    elif m < 0:
        return np.sqrt(2)*np.imag(psi(n, l, abs(m), r, elev, azim))

def probd(f):
    return np.abs(f)**2

#spherical coordinate to cartersian coordinate 
def sph2cart_probd(wavefunc, x:float, y:float, z:float)->float:
    #arctan가 아닌 arctan2를 사용해야 회전 방향을 알 수 있음
    r = np.sqrt(x**2 + y**2 + z**2)
    elev = np.arctan2(np.sqrt(x**2 + y**2), z)
    azim = np.arctan2(y, x)
    return probd(wavefunc(r, elev, azim))

from scipy.optimize import fsolve
import scipy.integrate 
def get_render_radius(n, l):
    #확률 밀도가 0.999인 반지름 구하기 
    f = lambda x : scipy.integrate.quad(lambda r : probd(r*R(n, l, r)), 0, x)[0] - 0.999
    return fsolve(f, 3*n)[0]
    
    def nomaliztion(x):
    temp = x + abs(x.min())
    return temp/temp.max()

def render_3d_cloud(ax, probd_func, radius, resol=70, rgb=(0.7, 0.3, 0.6)):
    X, Y, Z = np.meshgrid(np.linspace(-radius, radius, resol), np.linspace(-radius, radius, resol), np.linspace(-radius, radius, resol))
    P = probd_func(X, Y, Z)
    
    #making box
    scatter = ax.scatter3D(X, Y, Z, edgecolors="none", depthshade=False)
    
    #flatten
    xf = X.flatten()
    yf = Y.flatten()
    zf = Z.flatten()
    
    #RGBA weight
    wr = rgb[0] + 0.1*zf/abs(zf).max() + 0.1*xf/abs(xf).max() - 0.1*yf/abs(yf).max()
    wg = rgb[1] + 0.1*zf/abs(zf).max() + 0.1*xf/abs(xf).max() - 0.1*yf/abs(yf).max()
    wb = rgb[2] + 0.1*zf/abs(zf).max() + 0.1*xf/abs(xf).max() - 0.1*yf/abs(yf).max()
    wa = P.flatten()/P.max()

    wr = nomaliztion(wr)
    wg = nomaliztion(wg)
    wb = nomaliztion(wb)
    
    #coloring
    color_map = np.array([wr, wg, wb, wa]).T
    scatter.set_facecolor(color_map)

 

SP3

과정이 거의 비슷하기 때문에 SP3 오비탈만 소개한다.

#sp3 orbital
def h1(x, y, z):
    f = lambda r, elev, azim : 0.5*(o2s(r, elev, azim) + o2px(r, elev, azim) + o2py(r, elev, azim) + o2pz(r, elev, azim))
    return sph2cart_probd(f, x, y, z)

def h2(x, y, z):
    f = lambda r, elev, azim : 0.5*(o2s(r, elev, azim) - o2px(r, elev, azim) - o2py(r, elev, azim) + o2pz(r, elev, azim))
    return sph2cart_probd(f, x, y, z)

def h3(x, y, z):
    f = lambda r, elev, azim : 0.5*(o2s(r, elev, azim) - o2px(r, elev, azim) + o2py(r, elev, azim) - o2pz(r, elev, azim))
    return sph2cart_probd(f, x, y, z)

def h4(x, y, z):
    f = lambda r, elev, azim : 0.5*(o2s(r, elev, azim) + o2px(r, elev, azim) - o2py(r, elev, azim) - o2pz(r, elev, azim))
    return sph2cart_probd(f, x, y, z)

#h1
radius = get_render_radius(2, 1)

fig = plt.figure(dpi=300)
fig.subplots_adjust(right=0.5)
ax = fig.add_subplot(projection="3d")
ax.set_xlabel(r"$\frac{Z}{a}x$")
ax.set_ylabel(r"$\frac{Z}{a}y$")
ax.set_zlabel(r"$\frac{Z}{a}z$")
ax.set_title("Electron Cloud (SP3 h1)")

render_3d_cloud(ax, h1, radius, rgb=(0.7, 0.7, 0.4))
ax.view_init(elev=45, azim=45)

*matplotlib의 x,y축이 위에서 잡았던 것과 반대로 되어있다는 것을 감안하고 보아야 한다.

나머지는 비슷한 코드이니 생략함

radius = get_render_radius(2, 1)

fig = plt.figure(dpi=300)
fig.subplots_adjust(right=0.5)
ax = fig.add_subplot(projection="3d")
ax.set_xlabel(r"$\frac{Z}{a}x$")
ax.set_ylabel(r"$\frac{Z}{a}y$")
ax.set_zlabel(r"$\frac{Z}{a}z$")
ax.set_title("Electron Cloud (SP3)")

render_3d_cloud(ax, h1, radius, rgb=(0.7, 0.7, 0.4))
render_3d_cloud(ax, h2, radius, rgb=(0.7, 0.7, 0.4))
render_3d_cloud(ax, h3, radius, rgb=(0.7, 0.7, 0.4))
render_3d_cloud(ax, h4, radius, rgb=(0.7, 0.7, 0.4))
ax.view_init(elev=45, azim=45)

교과서같은 그림이 보일줄 알았는데, 구름이 너무 가까워서 공으로 보인다.

 

참고문헌

Atkins' Physical Chemistry 11e